斜率和积类模型
例1、已知椭圆C:,四点中三点恰有三点在椭圆上:
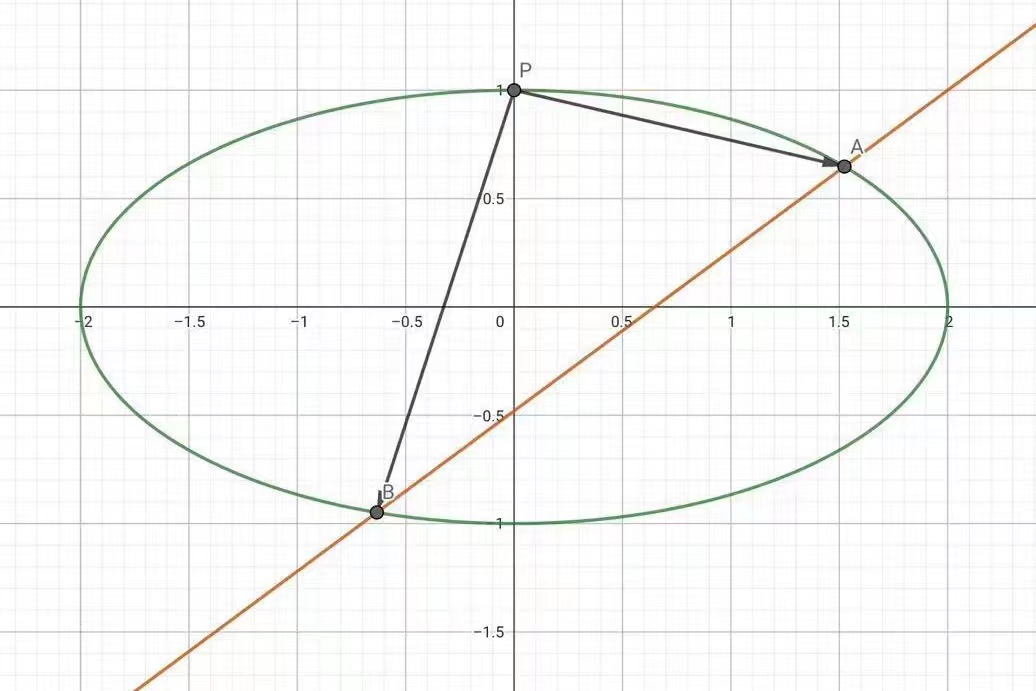
(Ⅰ)求椭圆的标准方程;
(Ⅱ)设直线不经过点且与C相交于A,B两点,若直线与的斜率的和为,证明:过定点。
解:不经过即
设A点坐标为为
故直线过定点
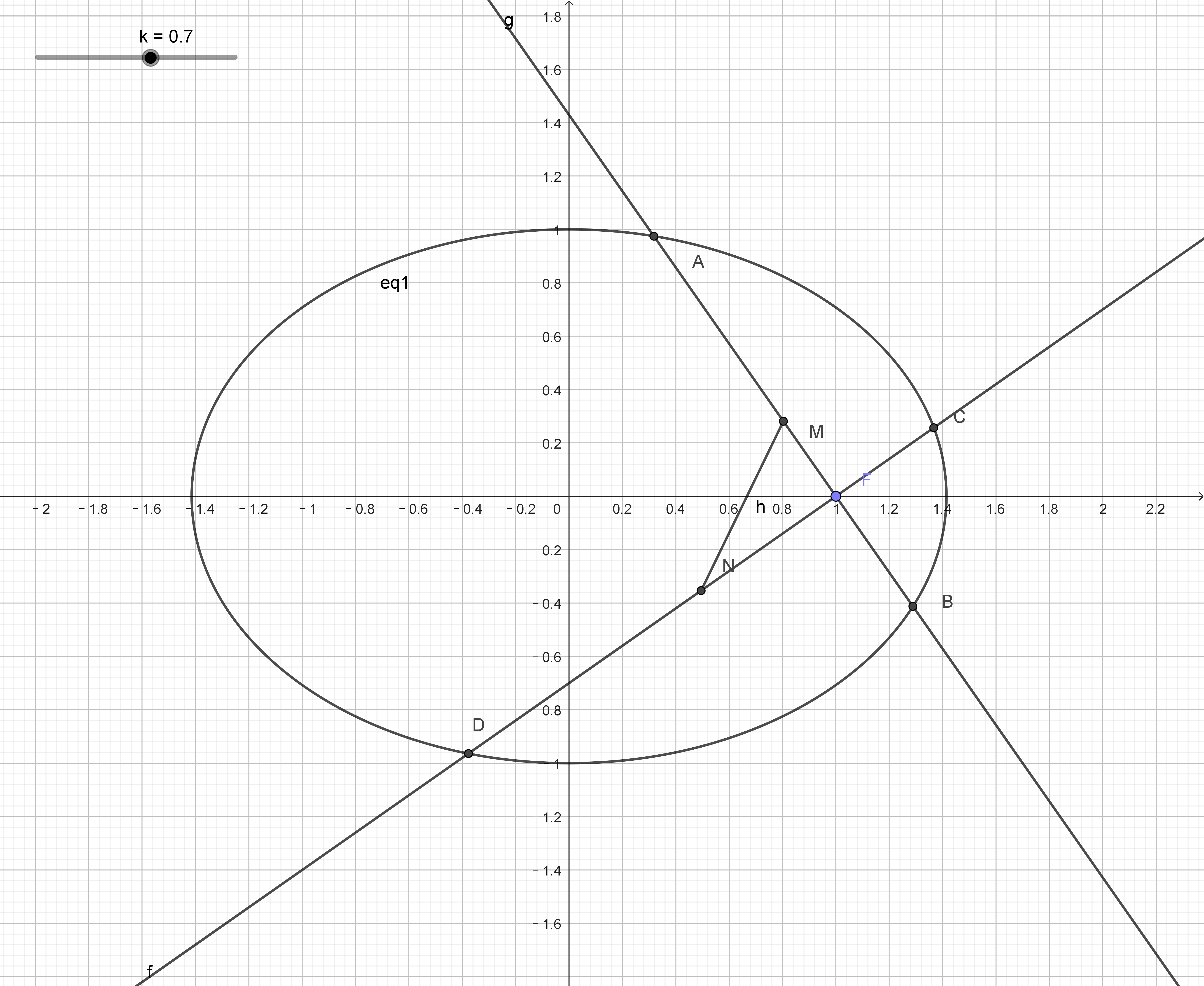
例2、(2024年成都期中试)已知椭圆右焦点
过F作两条互相垂直的弦AB、CD,设AB、CD的中点分别为M,N
(1)求椭圆的标准方程:
(2)证明:直线MN必过定点,并求出定点的坐标。
解:(2)设过F(1,0)的直线AB方程为,联立椭圆与直线的方程有:
同理设过F(1,0)的直线CD方程为,联立椭圆与直线的方程有:
设直线方程,与椭圆联立解得含m参数的M,N点坐标。
分析:因为动直线AB和CD均关于x轴对称,因而M,N也关于x轴对称,故动直线MN的定点一定在x轴,故有:
设直线MN与x轴的交点为(t,0)
这里用三点共线的斜率相等而不设立直线方程,目的是求解t值。如果是含m,则说明直线不经过定点。
例3、已知点和在双曲线:上,双曲线的左顶点为过点(且不与轴重合的直线与双曲线C交于两点,直线,与圆:分别交于于,两点。
(Ⅰ) 求双曲线的标准方程:
(Ⅱ)设直线AP、AQ的斜率分别为求的值
(Ⅲ)证明M、N过定点。
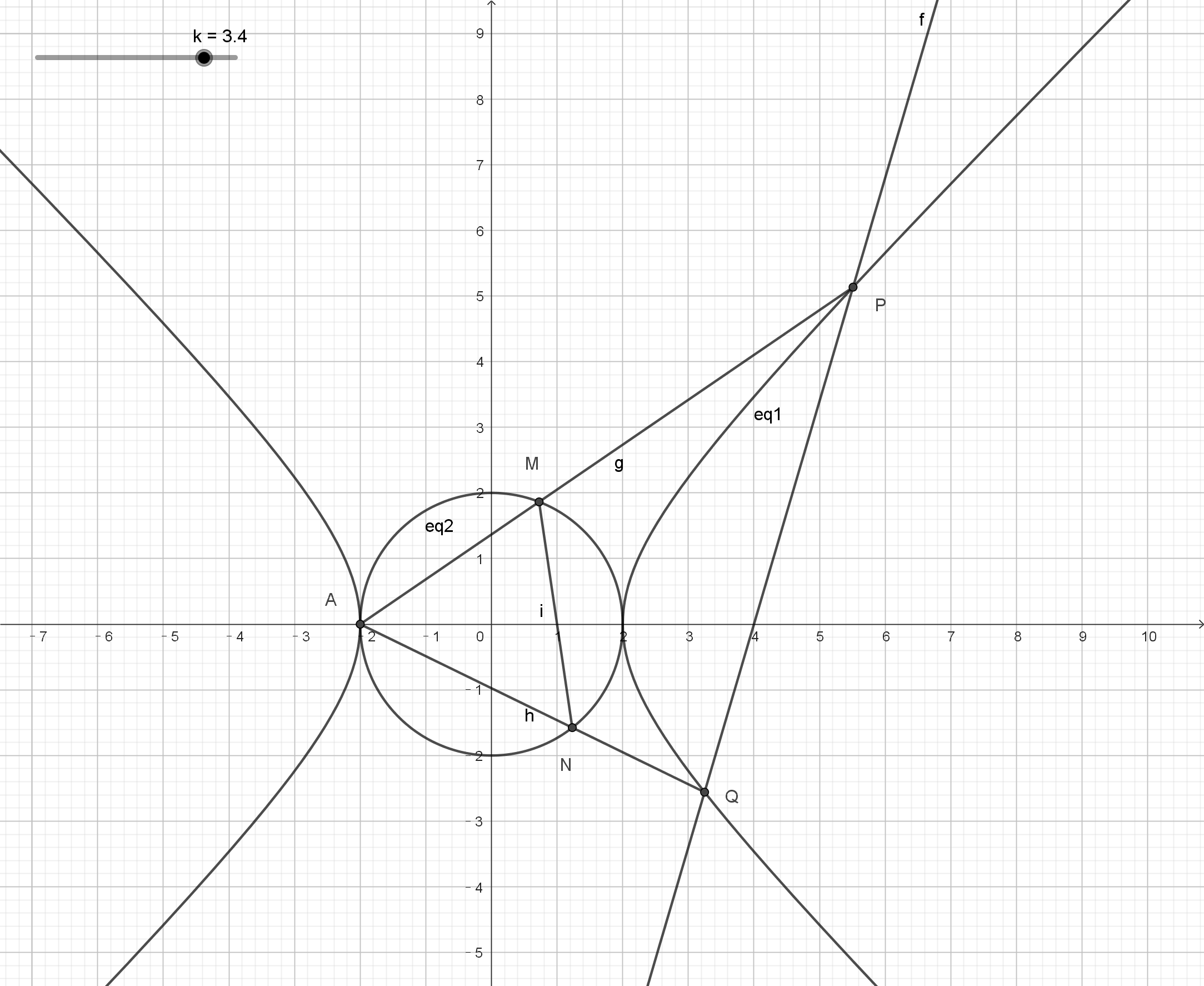
(Ⅱ)解:设过的直线:与联立,得设
分母=
(Ⅲ)圆的方程:,设过的直线方程为
分母=
=
直线过点
法二:平移齐次法
(Ⅱ)解:将点,椭圆向右平移两个单位,得到
椭圆平移后化简得
设经过L'(6,0)的直线方程:,设直线与椭圆的两个交点P
齐次化:
两边除得
,直线也过即,
(Ⅲ)圆向左平移两个单位,得,
设点直线的方程为
齐次化:
直线不过原点,两边除以
故直线过定点(3,0)






