**分四步,一、设点设直线,二、联立用韦达,三、三点共线用斜率关系列等式,四、根据极点刻意去配凑
用极点三角,计算出过n=1,配凑(n-1)的因式
拾之九八
例一:北京卷:已知椭圆 C:x28+y24=1
,与y轴的交点为A,B点A位于B的上方),直线
y=kx+4
与曲线C交于不同的两点连接交于点
M,N,连接AM,BN交于点G
,求证:点
G
纵坐标为定值。
预判:(0,4)点的极线为 点在此准线上
0⋅x8+4y4=1⇒y=1G点在此直线上
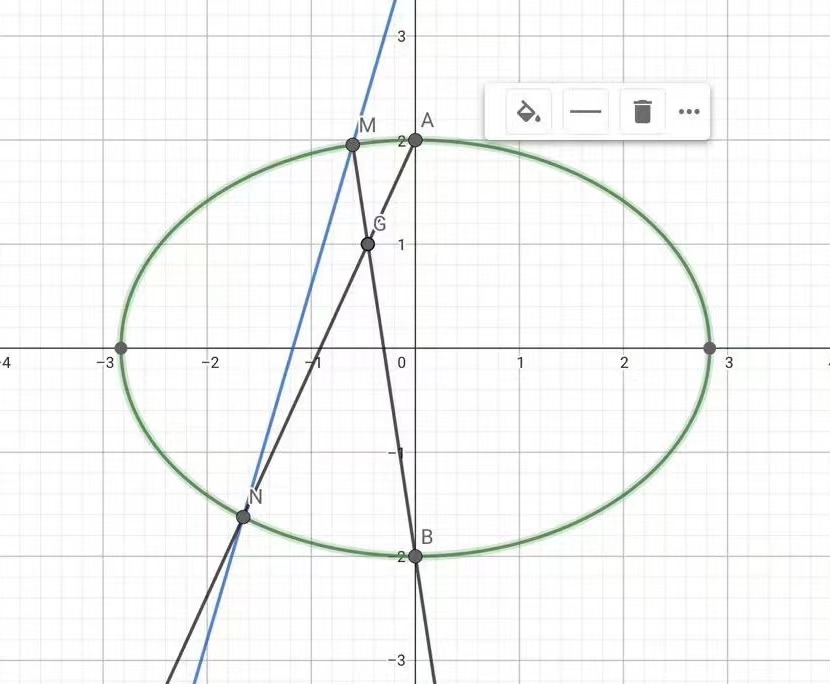
一、设点、设直线:
设三点直线
M(x1,y1),N(x2,y2),G(m,n),A(0,2),B(0,−2)直线lMN:y=kx+4
二、联立方程写韦达;
{y=kx+4×2+2y2−8=0⇒2(kx+4)2+x2−8=0⇒(2k2+1)x2+16kx+24=0
x1+x2=−16k2k2+1x1x2=242k2+1
三、三点共线用斜率列等式,
MBG三点共线:
y1+2×1=n+2m(1)
NAG三点共线:
y2−2×2=n−2m(2)
两式相除,得:
y1+2×1⋅x2y2−2=n+2n−2
四、交叉相乘再按需要配凑n-1:
(n+2)x1(y2−2)=(n−2)x2(y1+2)⇒(n+2)x1(kx2+2)=(n−2)x2(kx1+6)
⇒(n+2)kx1x2+2(n+2)x1=(n−2)kx2x1+6(n−2)x2
⇒4kx1x2+2(n−1+3)x1−6(n−1−1)x2=0
⇒2kx1x2+(n−1)(x1−3×2)+3(x1+x2)=0
⇒2k⋅242k2+1+(n−1)(x1−3×2)+3⋅−16k2k2+1=0⇒(n−1)(x1−3×2)=0
⇒n=1
G点定直线
y=1
上
例2:江苏卷例题:
x29+y25=1
左右顶点为A,B,设过点
T(t,m)
的直线
TA,TB
与椭圆分别交于其中设求证直线必过轴上的定点。
m(x1,y1),N(x2,y2),其中m>0,y1>0,y2<0.设t=9,求证直线MN必过x轴上的定点。
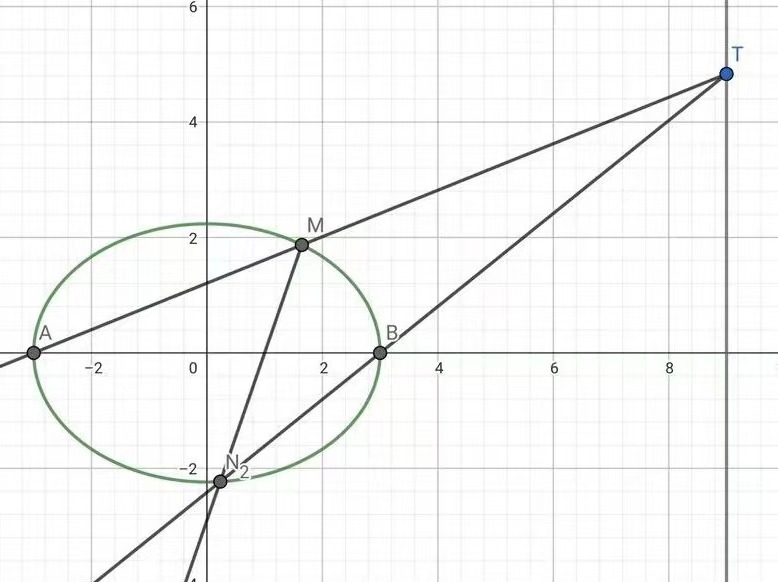
定点G(n,0)的极线为刻意构造
x=9,nx9+0⋅y5=1⇔x=9⇒n=1刻意构造n−1
一、设点设直线:
设设直线过定点点
M(x1,y1),N(x2,y2),设直线MN过定点点G(n,0),lMN=ty+nA(−3,0),B(3,)
·
二、联立方程
{x=ty+n5x2+9y2−5×9=0⇒5(ty+n)2+9y2−5×9=0
⇒(5t2+9)y2+10nt⋅y+5×(n2−9)=0
y1+y2=−10nt5t2+9y1y2=5(n2−9)5t2+9
三、三点共线斜率有等式
kAM=y1x1+3=m12=kTA(1)
kBN=y2x2−3=m6=kTB(2)
两式相除,得:
y1x1+3⋅x2−3y2=12∗
)
y2(x1+3)=2y1(x2−3)⇒x1y2+3y2=2x2y1−6y1
第四步:刻意构造(n-1)的因式分解式
从上式可以看出,消去x比消y简单一些。
⇒(ty1+n)y2+3y2=2(ty2+n)y1−6y1
⇒ty1y2+2(n−3)y1−(n+3)y2=0
⇒ty1y2+2(n−1−2)y1−(n−1+4)y2=0
ty1y2+(n−1)(2y1−y2)−4(y1+y2)=0
⇒t⋅5(n2−9)5t2+9+(n−1)(2y1−y2)−4⋅−10nt5t2+9=0
⇒5t(n2+8n−9)5t2+9+(n−1)(2y1−y2)=0
⇒(n−1)⋅[5t(n+9)5t2+9+(2y1−y2)]=0
⇒n−1=0∴
n=1,直线过定点G(1,0)
对第四步的处理还有以下两种方法:
法二、
利用椭圆第三定义对非对称韦达定理处理 利用椭圆第三定义对非对称韦达定理处理
y1x1+3⋅x2−3y2=12
kAM⋅kBM=−b2a2=−59
kAM=y1x1+3=−59⋅1kBM=−59⋅x1−3y1
y1x1+3⋅x2−3y2=−59⋅x1−3y1⋅x2−3y2=12
x1−3y1⋅x2−3y2=x1x2−3(x1+x2)+9y1y2
x1x2=(ty1+n)(ty2+n)=t2y1y2+nt(y1+y2)+n2
−3(x1+x2)=−3(ty1+n+ny2+n)=−3t(y1+y2)−6n
分子
分子=t2y1y2+t(n−3)(y1+y2)+n2−6n+9
x1x2−3(x1+x2)+9y1y2=t2y1y2+t(n−3)(y1+y2)+(n−3)2y1y2
=t2⋅5(n2−9)+t(n−3)(−10nt)+(n−3)2(5t2+9)5(n2−9)
∵y1+y2=−10nt5t2+9y1y2=5(n2−9)5t2+9
5n2t2−5⋅9t2−10n2t2+30nt2+5n2t2−30nt2+9⋅5t2+9(n−3)25(n2−9)
(
=9(n−3)25(n+3)(n−3)=−95⋅12
⇒n−3n+3=−12⇒n=1
法三、韦达定理的和积互化处理非对称韦达定理。
y1x1+3⋅x2−3y2=12=
y1(ty2+n−3)y2(ty1+n+3)=ty1y2+(n−3)y1ty1y2+(n+3)y2
∵y1+y2=−10nt5t2+9y1y2=5(n2−9)5t2+9
令
y1y2=λ⋅(y1+y2)⇒λ=n2−9−2nt
ty1y2+(n−3)y1ty1y2+(n+3)y2=t⋅n2−9−2nt(y1+y2)+(n−3)y1t⋅n2−9−2nt(y1+y2)+(n+3)y2
=
(n2−9)⋅(y1+y2)−2n(n−3)y1(n2−9)(y1+y2)−2n(n+3)y2=(n−3)⋅[(n+3)(y1+y2)−2ny1](n+3)⋅[(n−3)(y1+y2)−2ny2]
=(n−3)⋅[y1(3−n)+y2(n+3)](n+3)⋅[y1(n−3)−y2(n+3)]=−n−3n+3=12
∴n=1



